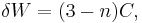Cotton tensor
In differential geometry, the Cotton tensor on a (pseudo)-Riemannian manifold of dimension n is a third-order tensor concomitant of the metric, like the Weyl tensor. The concept is named after Émile Cotton. Just as the vanishing of the Weyl tensor for n ≥ 4 is a necessary and sufficient condition for the manifold to be conformally flat, the same is true for the Cotton tensor for n = 3, while for n < 3 it is identically zero.
In coordinates, and denoting the Ricci tensor by Rij and the scalar curvature by R, the components of the Cotton tensor are
The Cotton tensor can be regarded as a vector valued 2-form, and for n=3 one can use the Hodge star operator to convert this in to a second order trace free tensor density
sometimes called the Cotton–York tensor.
The proof of the classical result that for n = 3 the vanishing of the Cotton tensor is equivalent the metric being conformally flat is given by Eisenhart using a standard integrability argument. This tensor density is uniquely characterized by its conformal properties coupled with the demand that it be differentiable for arbitrary metrics, as shown by Aldersley.
Contents |
Properties
Conformal rescaling
Under conformal rescaling of the metric 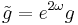 for some scalar function
for some scalar function  the Cotton-York tensor transforms as
the Cotton-York tensor transforms as
where the gradient is plugged into the symmetric part of the Weyl tensor W.
Symmetries
The Cotton tensor has the following symmetries:
and therefore
In addition the Bianchi formula for the Weyl tensor for can be rewritten as
where 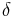 is the positive divergence in the first component of W.
is the positive divergence in the first component of W.
References
- Aldersley, S. J. (1979). "Comments on certain divergence-free tensor densities in a 3-space". Journal of Mathematical Physics 20 (9): 1905–1907. Bibcode 1979JMP....20.1905A. doi:10.1063/1.524289.
- Cotton, É. (1899). "Sur les variétés à trois dimensions". Ann. Fac. Sci. Toulouse. II 1 (4): 385–438. http://www.numdam.org/numdam-bin/fitem?id=AFST_1899_2_1_4_385_0.
- Eisenhart, Luther P. (1977) [1925]. Riemannian Geometry. Princeton, NJ: Princeton University Press. ISBN 0691080267.
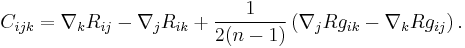
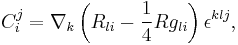
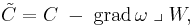
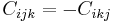
![C_{[ijk]} = 0. \,](/2012-wikipedia_en_all_nopic_01_2012/I/6080af73c2211582c049f7ae62573872.png)